Bunderan (élmu ukur)

Dina géométri Euklid, hiji bunderan nyaéta kumpulan sakabéh titik dina hiji widang dina jarak nu tangtu, anu disebut radius, ti hiji titik nu tangtu, anu disebut puseur. Bunderan nyaéta conto tina kurva nutup basajan, ngabagi widang jadi bagian jero jeung bagian luar.

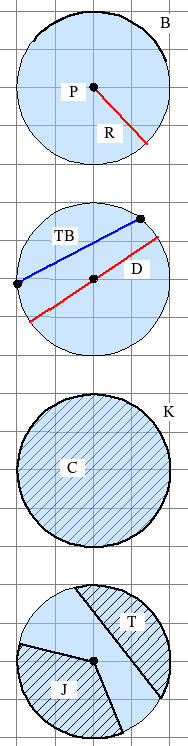
Bagian-bagian tina hiji bunderan.

Bagian-bagian bunderan

Bagian-bagian anu aya dina bunderan, nyaéta:

• Bagian bunderan anu mangrupa titik, nyaéta:
  1. Titik puseur (P) mangrupa hiji titik dina jero bunderan anu jadi rujukan pikeun nangtukeun jarak ka kumpulan titik anu ngawangun bunderan antukna sarua. Jarak antara titik puseur jeung bunderan hargana tetep sarta disebut radius.
• Bagian bunderan anu mangrupa garis, nyaéta:
  1. Radius (R) mangrupa garis lempeng anu nyambungkeun titik puseur jeung bunderan.
  2. Tali gondéwa mangrupa garis lempeng dina jero bunderan anu motong bunderan dina dua titik anu béda (TG) atawa tali busur (TB) (dina basa Indonesia).
  3. Gondéwa (G) atawa busur (dina basa Indonesia) mangrupa garis melengkung anu patindih jeung bunderan.
  4. Kuriling bunderan (K) mangrupa gondéwa pangpanjangna dina bunderan.
  5. Diaméter (D) mangrupa tali gondéwa pangpanjangna nyaéta dua kali ti radiusna. Diaméter ieu ngabagi dua bunderan nu sarua legana.
• Bagian bunderan anu mangrupa lega, nyaéta:
  1. Juring (J) mangrupa wewengkon dina bunderan anu diwatesan ku gondéwa sarta dua radius anu aya dina dua tungtungna.
  2. Tambéréng (T) mangrupa wewengkon dina bunderan anu diwatesan ku hiji gondéwa sarta tali gondéwana.
  3. Cakram (C) mangrupa sakabéh wewengkon anu aya dina jero bunderan. Legana nyaéta radius kuadrat dikalikeun jeung pi. Cakram mangrupa juring panglegana.

Persamaan

Hiji bunderan mibanda persamaan:

$(x-x_{0})^{2}+(y-y_{0})^{2}=R^{2}\!$

di mana $R\!$ nyaéta radius bunderan sarta $(x_{0},y_{0})\!$ nyaéta koordinat puseur bunderan.

Persamaan paramétrik

Bunderan bisa ogé dirumuskeun dina hiji persamaan paraméterik, nyaéta

$x=x_{0}+R\cos(t)\!$

$y=y_{0}+R\sin(t)\!$

anu lamun diantepkeun ngaliwatan waktu t baris dijieun hiji galur nu ngawangun bunderan dina rohang x-y.

Lega bunderan

Lega bunderan mibanda rumus:

$A=\pi R^{2}\!$

anu bisa diturunkeun jadi:

$dA=rd\theta \ dr$

dina koordinat polar, nyaéta

$\int da=\int _{r=0}^{R}\int _{\theta =0}^{2\pi }rd\theta \ dr$

$=\int _{r=0}^{R}rdr\int _{\theta =0}^{2\pi }d\theta$ $={\frac {1}{2}}(R^{2}-0^{2})\ (2\pi -0)=\pi R^{2}\!$

Ku cara anu sarua bisa ogé diitung lega satengah bunderan, saparapat bunderan, sarta bagian-bagian bunderan. Ogé bisa diitung lega hiji cincin bunderan kalawan radius jero $R_{1}\!$ sarta radius luar $R_{2}\!$.

Pangjumlahan bagian juring

Lega bunderan bisa diitung ku cara ngabagi-bagi bunderan jadi juring-juring nu saterusna disusun deui jadi hiji pasagi panjang anu legana bisa ditangtukeun kalawan gampang. Dina gambar r hartina sarua jeung R nyaéta radius bunderan.

Lega juring

Lega juring hiji bunderan bisa diitung lamun lega bunderan dijadikeun fungsi tina R jeung θ, nyaéta;

$A(R,\theta )={\frac {1}{2}}R^{2}\theta \!$

kalayan wates harga θ nyaéta antara 0 jeung 3π. Waktu θ boga harga 2π, juring anu diitung nyaéta juring panglegana, atawa lega bunderan.

Lega cincin

Hiji cingcin mibanda lega anu gumantung kana radius jero $R_{1}\!$ sarta radius luar $R_{2}\!$, nyaéta

$A_{cincin}=\pi (R_{2}^{2}-R_{1}^{2})\!$

di mana pikeun $R_{1}=0\!$, rumus ieu jadi jadi rumus lega bunderan.

Lega potongan cincin

Ku cara ngagabungkeun dua rumus saméméhna, bisa dibeunangkeun

$A_{potongan\ cincin}={\frac {\pi }{2}}(R_{2}^{2}-R_{1}^{2})\theta \!$

anu mangrupa lega hiji cingcing teu gembleng.

Kuriling bunderan

Kuriling bunderan mibanda rumus:

$L=2\pi R\!$

Panjang gondéwa bunderan

Panjang gondéwa hiji bunderan bisa diitung kalawan ngagunakeun rumus:

$L=R\theta \!$

anu diturunkeun ti rumus pikeun ngitung panjang hiji kurva:

$dL=\int {\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}dx\!$

di mana dipaké

$y=\pm {\sqrt {R^{2}-x^{2}}}\!$

minangka kurva anu nyusun bunderan. Tanda \pm ngisaratkeun yén aya dua kurva (pelengkungan), nyaéta bagian luhur jeung bagian handap. Duanana idéntik (inget définisi bunderan), ku kituna sabenerna ngan perlu diitung sakali sarta hasilna dikalikan dua.

Pi atawa π

Harga pi nyaéta hiji angka anu mangrupa sipat husus tina bunderan, nyaéta babandingan antara kuriling K jeung diaméternya D:

$\pi ={\frac {K}{D}}$