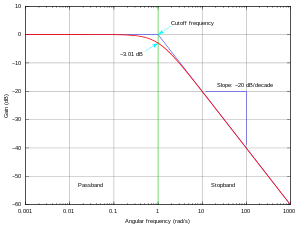
Cutoff frequency
Dina élmu fisika jeung téknik listrik, istilah cutoff frequency luhur atawa handap, frékuénsi juru, jeung bréak frequency ngagambarkeun hiji wates dina réspon frékuénsi hiji sistem di mana énergi nu asup kana sistem kasebut mimiti diaténuasi atawa malah dipantulkeun lain ditransmisikeun. Conto umumna:

|
|
Artikel ieu keur dikeureuyeuh, ditarjamahkeun tina basa Inggris. Bantuanna didagoan pikeun narjamahkeun. |
- a cutoff frequency of an idéal lowpass, highpass, bandpass or Band-stop filter, i.e. discrete point in the magnitude transfer function, a frequency where a passband and a stopband meets.
- the passband frequency limits of an electronic circuit such as a filter or an amplifier, i.e. the point in the filter specification where the transition band and the passband meets; defined as the 3 dB cutoff frequencies, i.e. the lowest or the highest frequency for which the output of the circuit deviates less than typically 3 dB from the nominal passband value.
- the stopband corner frequencies or limit frequencies of a filter, i.e. the point where the transit band and the stopband meets; either the lowest or the highest frequency for which the attenuation is larger than the required stopband attenuation, which for example may be 30 dB or 100 dB.
- the upper or lower 3 dB cutoff frequencies of a communication channel. In the case of a waveguide or an antenna, this corresponds to the lower and upper cutoff wavelengths respectively.
- the 3 dB cutoff frequency of a signal spectrum, for example of a baseband signal or a passband signal.
The cutoff frequency can also refer to the plasma frequency, or to some concepts related to renormalization in quantum field theory.
Electronics
éditIn electronics, cutoff frequency or corner frequency is the frequency either above which or below which the power output of a circuit, such as a line, amplifier, or electronic filter is the power of the passband.[1] Because power is proportional to the square of voltage, the voltage signal is of the passband voltage at the corner frequency. Hence, the corner frequency is also known as the −3 dB point because is close to −3 decibels. A bandpass circuit has two corner frequencies; their geometric mean is called the center frequency.
Communications
éditIn communications, the term cutoff frequency can méan the frequency below which a radio wave fails to penetrate a layer of the ionosphere at the incidence angle required for transmission between two specified points by reflection from the layer.
Waveguides
éditThe cutoff frequency of an electromagnetic waveguide is the lowest frequency for which a mode will propagate in it. In fiber optics, it is more common to consider the cutoff wavelength, the maximum wavelength that will propagate in an optical fiber or waveguide. The cutoff frequency is found with the characteristic equation of the Helmholtz equation for electromagnetic waves, which is derived from the electromagnetic wave equation by setting the longitudinal wave number equal to zero and solving for the frequency. Thus, any exciting frequency lower than the cutoff frequency will attenuate, rather than propagate. The following derivation assumes lossless walls. The value of c, the speed of light, should be taken to be the group velocity of light in whatever material fills the waveguide.
For a rectangular waveguide, the cutoff frequency is
where are the mode numbers and a and b the lengths of the sides of the rectangle.
The cutoff frequency of the TM01 mode in a waveguide of circular cross-section (the transverse-magnetic mode with no angular dependence and lowest radial dependence) is given by
where is the radius of the waveguide, and is the first root of , the bessel function of the first kind of order 1.
For a single-mode optical fiber, the cutoff wavelength is the wavelength at which the normalized frequency is approximately equal to 2.405.
Mathematical analysis
éditThe starting point is the wave equation (which is derived from the Maxwell equations),
which becomes a Helmholtz equation by considering only functions of the form
Substituting and evaluating the time derivative gives
The function here refers to whichever field (the electric field or the magnetic field) has no vector component in the longitudinal direction - the "transverse" field. It is a property of all the eigenmodes of the electromagnetic waveguide that at léast one of the two fields is transverse. The z axis is defined to be along the axis of the waveguide.
The "longitudinal" derivative in the Laplacian can further be reduced by considering only functions of the form
where is the longitudinal wavenumber, resulting in
where subscript T indicates a 2-dimensional transverse Laplacian. The final step depends on the géometry of the waveguide. The éasiest géometry to solve is the rectangular waveguide. In that case the remainder of the Laplacian can be evaluated to its characteristic equation by considering solutions of the form
Thus for the rectangular guide the Laplacian is evaluated, and we arrive at
The transverse wavenumbers can be specified from the standing wave boundary conditions for a rectangular géometry crossection with dimensions a and b:
where n and m are the two integers representing a specific eigenmode. Performing the final substitution, we obtain
which is the dispersion relation in the rectangular waveguide. The cutoff frequency is the critical frequency between propagation and attenuation, which corresponds to the frequency at which the longitudinal wavenumber is zero. It is given by
The wave equations are also valid below the cutoff frequency, where the longitudinal wave number is imaginary. In this case, the field decays exponentially along the waveguide axis.
Tempo ogé
éditRujukan
édit- ↑ Van Valkenburg, M. E. Network Analysis (3rd edition ed.). pp. pp. 383–384. ISBN 0-13-611095-9. Diakses tanggal 2008-06-22.

